Ask Ethan: How do symmetries lead to conservation laws? | by Ethan Siegel | Starts With A Bang! | Apr, 2024
First derived by Emmy Noether, for every symmetry a theory possesses, there’s an associated conserved quantity. Here’s the profound link.
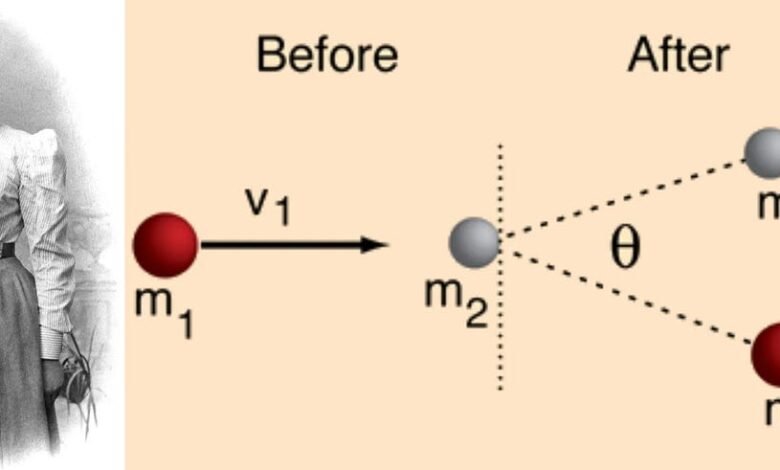
In this Universe, there are certain physical quantities that are — quite importantly — always conserved. Laws like the “conservation of energy,” “conservation of momentum,” and “conservation of angular momentum” are cornerstones of theories ranging from Newtonian mechanics all the way to quantum electrodynamics and beyond, and apply equally to planets in the Solar System as they do to collisions taking place inside the world’s most powerful particle accelerators. But these aren’t just empirical laws that we observe to be true; they’re an inevitable consequence of certain symmetries that these theories exhibit: an unavoidable connection required by Noether’s Theorem.
What’s the connection? That’s the topic of this week’s question from Kaleberg, who enjoyed this prior article on symmetries in physics and inquired with this follow-up:
“Excellent. Now do an article on Noether’s Theorem and show how symmetry leads to conservation laws. Doesn’t spatial invariance imply conservation of momentum, and doesn’t time invariance imply conservation of energy?”
Beyond the fact that symmetries exist, there’s an incredible connection between symmetries and conserved quantities, and it’s one of the deepest physical insights to come out of all of physics history.
Back in 1918, something fascinating occurred in the world of mathematics. Just a few years after the publication of Einstein’s General Relativity — which changed how we viewed gravitation, spacetime, and the behavior of the Universe itself — people were puzzling over a seemingly peculiar fact. In the general theory of relativity, energy conservation didn’t appear as a natural consequence that was “baked into” the fabric of spacetime itself, but rather only appeared as an identity. David Hilbert, one of the foremost mathematicians of the time, wondered how, then, it was possible to constrain…
Source link




